Sourcerer: Maximum Entropy Source Distribution Estimation

Monday. February 12, 2024 - 2 mins

Inference is the common task of finding the posterior distribution over parameters consistent with a specific outcome (or set of outcomes) from a model. What about the case where you have several outcomes, all coming from the same model, but from different parameters? We want to find a distribution over the parameters that is consistent with all observations. This is the Source Distribution Estimation Problem, also commonly known as Empirical Bayes (EB).

More concretely, we have a simulator model taking parameters $\theta$ and generates potential outcomes $x$ by sampling from the implicit likelihood $p(x\vert\theta)$. We are given a distribution $p_0(x)$ (or samples from this distribution), and want to find a distribution $s(\theta)$ which satisfies

\[s^{\#}(x) = \int p(x\vert\theta)s(\theta)d\theta = p_0(x)\]

for all $x$.

The problem? The distribution $s(\theta)$ is not unique! There can be more than one distribution $s(\theta)$ which is “pushed forward” to the same distribution $p_0(x)$.

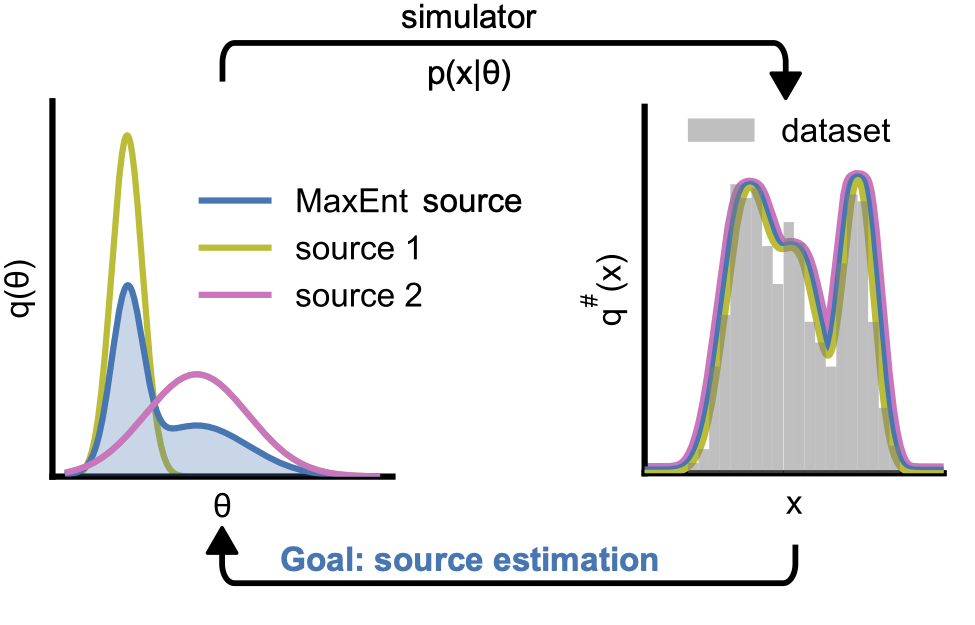
Screenshot

We resolve this by tackling the maximum entropy source distribution - which we show to be unique. We argue this is intuitively a good target, as the maximum entropy distribution is guaranteed to cover all feasible parameter configurations, and so we don’t miss any “good” parameters. In practice, we approximate the maximum entropy distribution by training a variational distribution to minimize a convex combination of the entropy, and a distance measure between the real data distribution $p_0(x)$ and the estimated pushforward $s^{\#}(x)$:

\[\mathcal{L} = \lambda H (s) - (1-\lambda) D_{\text{SW}}(s^{\#},p_0)\]

Where $D_{\text{SW}}$ is the Sliced-Wasserstein Distance, which is a scalalbe measure of distance between distributions coming from optimal transport (see, e.g., Kimia Nadjahi’s excellent thesis).

With these components, we are able to estimate source distributions in a fast and sample-based fashion! Best of all, we see that adding the entropy term to the loss gives us higher entropy distributions for free - we don’t pay a price for our higher entropy distributions in terms of how close our simulations are to the dataset. This is true even for complex, high-dimensional simulators such as the Hodgkin-Huxley model from neuroscience.

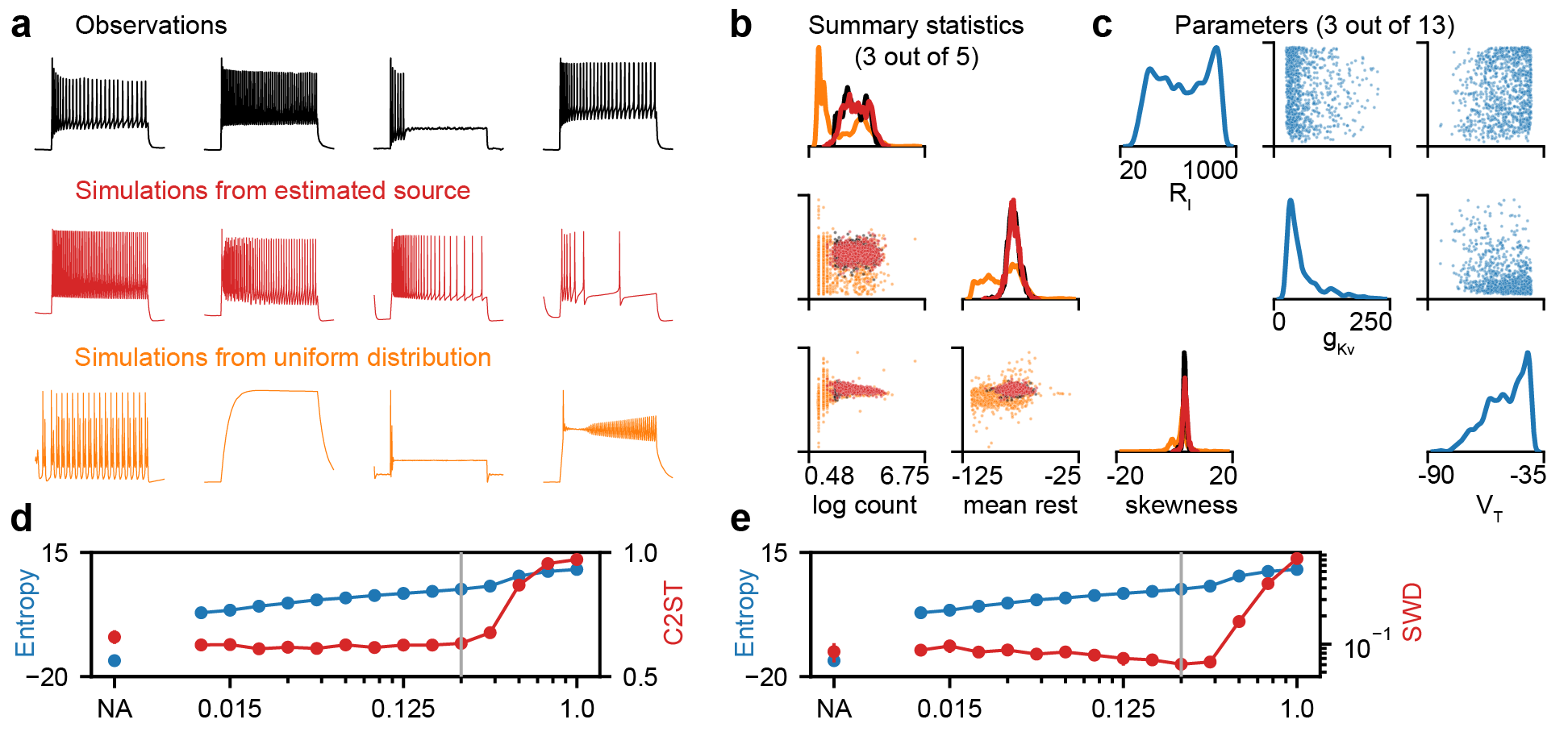
Screenshot

If this sounds interesting to you, feel free to get in touch! Also, check out the full paper and the great blog post about it from TransferLab!