FNOPE: Simulation-based inference on function spaces with Fourier Neural Operators
- 2 minsSimulation-based inference enables inference, in principle, for any black-box model. That is, as long as you can provide a simulation dataset, you pick a model from the family of sbi methods, train it, and plug in your posterior. However, when you have many parameters, this becomes more complicated. This is because training generative models in high-dimensional spaces is hard. When I set out to solve an inference problem in Glaciology, I found that this limitation can very quickly become a problem. This is because in geoscience, the simulator parameters are not vector-valued quantities (that is, a finite set of variables describing discrete properties of the system). Instead, the parameters are function-valued, because they describe quantities that vary in space and time. This makes the parameter dimensionality explode very quickly, and most SBI methods simply cannot be scaled to these dimensionalities. However, the intrinsic dimensionality of the problem may not be that much higher - typically variables that vary in space and time are strongly correlated. In this work, we set out to define an SBI method that is tailored to function-valued parameters. Concretely, we had two goals:
- Our method should scale well (in terms of simulation efficiency) with increasing number of parameters.
- Our method should be amortized across discretizations of the domain.
The latter requirement is a practical one. Amortization is an immensely useful property of simulation-based inference. However, when making geophysical measurements, it is often not possible to measure on the same nice, equispaced, fixed grid that we run our simulations on. This is a friendly reminder I always received from my collaborators in the field, driving skidoos across Antarctic Ice Shelves to collect data to use in our inference workflows.
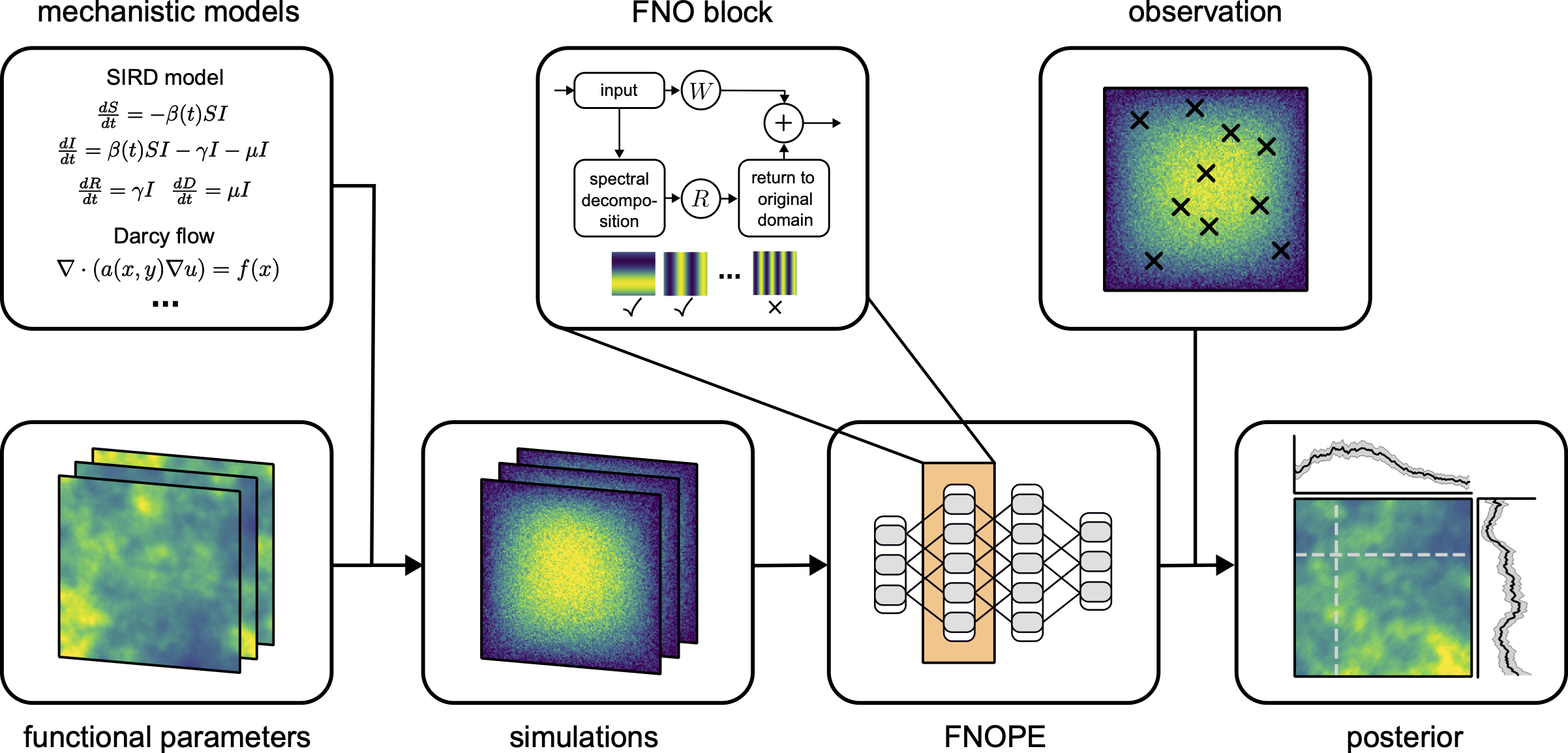
To achieve these two goals, we developed an SBI method using Fourier Neural Operators (FNOs). FNOs operate on the Fourier modes of the data, discarding higher frequency modes. This is a strong assumption on the correlation of the parameters, but it is very commonly applicable in geoscientific applications. This assumption allows for a fixed representation of the parameters, regardless of the number of points in our space/time domain, achieving requirement 1. Second, we introduce additional noise and masking during training to emulate different discretizations, even for simulators which take fixed discretizations. This allows us to robustly condition our network on any discretization of the parameters and observations, achieving requirement 2. With our method, we solve inference problems with parameters defined as functions over a 2D spatial domain, even using smaller simulation budgets.
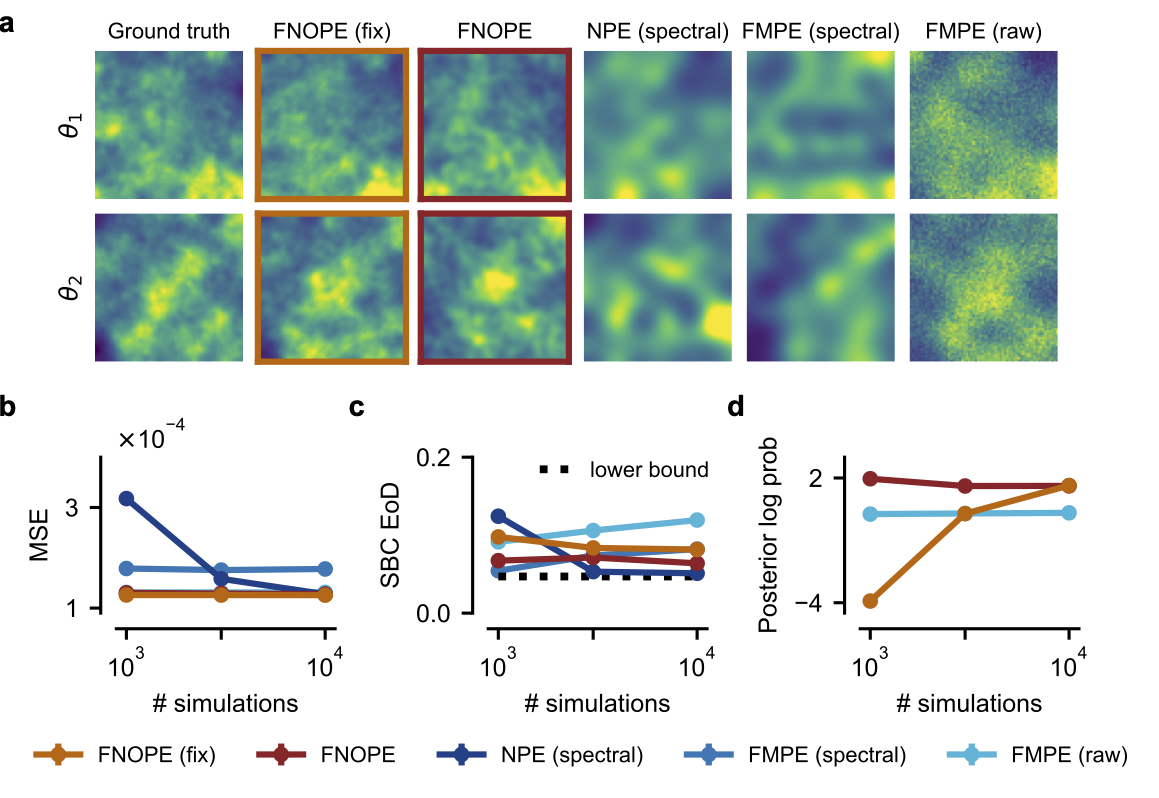
This was an incredibly fun and fulfilling project to work on, and I am very optimistic about the future of this method and extensions as tools of inference in geoscience. If this work sounds interesting to you, check out the paper, to be published at NeurIPS, as well as the code, or get in touch!